Fra le caratteristiche peculiari di SecondLife c’è l’importante fatto che può essere utilizzata come una palestra di apprendimento, sperimentazione e verifica delle proprietà geometriche dello spazio tridimensionale in cui viviamo. L’opportunità è ghiotta perchè consente di vedere immediatamente l’effetto di equazioni, in un modo rapido ed efficace come nessun programma tradizionale potrebbe consentire.

Anche al di là dell’educational, è utile per tutti coloro che vogliono creare ed animare cose in SL o in programmi di animazione, conoscere le basi della trigonometria, che consentono di capire e riprodurre come avvengono gli spostamenti lungo traiettorie curve. Vi sembrerà strano ma molti scripter entrano in crisi quando gli si chiede di far compiere ad un oggetto una traiettoria circolare, soprattutto se si vuole che questa traiettoria possa essere calcolata indipendentemente dalla rotazione iniziale del pezzo.

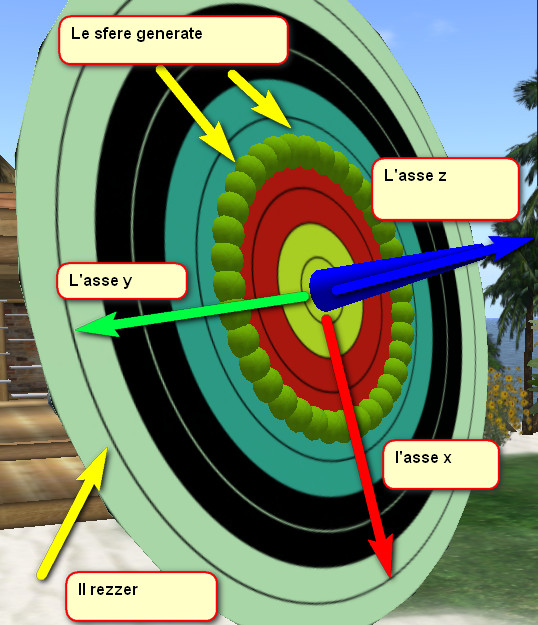
Negli anni passati questo problema mi era stato chiesto cercando di simulare in SL lo spostamento dei sedili di una ruota panoramica. Gli script disponibili in quel momento consentivano di far “ruotare” la ruota, ma soltanto se la ruota era allineata lungo una certa direzione (es. NS), se la ruota veniva rezzata e “girata” per farla stare in una sim diversa, la rotazione era quella “standard” e quindi con i sedili che si muovevano lungo un cerchio diverso rispetto ai sostegni. Vi lascio solo immaginare inoltre l’inutile complessità degli script generati che cercavano di “cucinare” seni e coseni cercando di ottenere il risultato sperato.

La soluzione matematicamente esatta

Ora la soluzione al problema di tracciare un cerchio nello spazio 3D con il cosiddetto metodo “parametrico” (vale a dire facendo variare un parametro t in un certo intervallo e calcolando le componenti x,y,z per ogni valore), è persino molto elegante ed è riassumibile dalla seguente equazione:

Dove R è il raggio del cerchio, c rappresenta le coordinate del centro del cerchio, u è un vettore unitario che punta arbitrariamente dal centro verso un punto della circonferenza e n è il vettore unitario normale al cerchio.

Oppure nella versione più semplice (se si hanno già due vettori perpendicolari come vedremo è questo il caso in SL):

Che l’equazione sia elegante, non c’è dubbio (ci sono infatti un sacco di segni strani), per capirla dobbiamo fare un piccolo excursus sulla famigerata “trigonometria”. Quindi cerchiamo di fare un piccolo riepilogo dalle basi per cercare di capirla. (NB: notate che per ottenere questa formula ho dovuto ricercare molto intensamente tutto il materiale infinito presente in rete, perchè non è di quelle equazioni che si trovano facilmente su wikipedia). Io l’ho rintracciata in questo forum di fisica: http://www.physicsforums.com/showthread.php?t=123168.

Definizione di base della trigonometria.

Se guardiamo il famoso “cerchio trigonometrico”, che definisce le funzioni seno e coseno in funzione di una circonferenza di raggio unitario:

Capite la profonda elementare relazione che lega seni/coseni con il cerchio appunto. La componente X delle coordinate di un cerchio è appunto Rcos A, mentre la componente Y di coordinate vale Rsin A dove A è l’angolo.

Da questo schema si capisce che per poter descrivere una circonferenza è sufficiente prendere un angolo A e farlo scorrere fra 0 e 360 gradi: plottando le coordinate X e Y definite come RcosA e RsinA viene descritta appunto l’intera circonferenza.

Ma come applicare questo in 3D?

Per poter disegnare questa circonferenza in uno spazio tridimensionale, occorre definire in qualche modo le coordinate X’ e Y’ che descrivono il piano complanare a dove vogliamo disegnare il cerchio nello spazio 3D.

Se abbiamo quindi due vettori unitari U e V che “fungano” da assi cartesiani (siano quindi perpendicolari fra di loro), allora l’equazione del cerchio sarà qualcosa tipo RcosA*U+RsinA*V.

L’applicazione in SL

Supponiamo di avere un oggetto che abbia i propri assi locali X (asse rosso), Y (asse verde), Z (asse blu) e di volere disegnare un cerchio. Abbiamo già i vettori perpendicolari che ci interessano. Per la cronaca usando il linguaggio di scripting per ottenere i vettori normalizzati lungo l’asse X e Y basta fare:

vector v=llVecNorm(llRot2Left(llGetRot())); // torna il vettore unitario dell’oggetto lungo l’asse Y che in SL è il vettore “a sinistra”
vector u=llVecNorm(llRot2Fwd(llGetRot())); // torna il vettore unitario dell’oggetto lungo l’asse X che in SL è il “forward” cioè il fronte dell’oggetto

e per plottare la circonferenza basta fare ad esempio il seguente ciclo:

for(angle=0;angle<360;angle+=10)
{
float rad=DEG_TO_RAD*angle;
vector pos=R*llCos(rad)*u+R*llSin(rad)*(v)+center;
plot(pos);
}

che “plotta” un punto incrementando ogni volta di 10 gradi. Notate che l’angolo “volgare” 0-360 viene moltiplicato per la costante  DEG_TO_RAD per ottenere il corrispondente valore in radianti, che è l’unità di misura “giusta” per operare con le funzioni seno e coseno.

A proposito del plot

Cosa significhi “plottare” in 3D in SecondLife? Ci sono diverse tecniche. Quella che ho seguito io consiste nel “rezzare” una palla alle coordinate indicate. La palla è meglio che sia “temporanea” in modo da scomparire autonomamente dopo circa 1-2 minuti.

Lo script di plot risulta pertanto niente di più che il seguente:

plot(vector x)
{
llRezObject(“Sphere”,x,ZERO_VECTOR,ZERO_ROTATION,0);

}

Per avere una copia di questo rezzer basta che mi mandiate un IM in SL oppure una email a Salahzar@gmail.com

NB: Ci sono molte applicazioni che si possono fare a partire da questo semplice rezzer: non ultimi i rezzer di collane o di strutture di edifici. Inoltre queste equazioni possono come detto essere base per la realizzazione di sentieri curvi su cui far muovere treni ascensori etc…

Salahzar